6427. Пчелиные ульи
Пчелы являются
одними из самых трудолюбивых насекомых. Так как они собирают нектар и пыльцу с
цветов, то должны ориентироваться по деревьям в лесу. Для простоты n деревьев пронумерованы числами от 0 до
n – 1. Вместо того, чтобы бродить по
лесу, они используют особый список путей. Путь соединяет два дерева, между
которыми пчелы могут двигаться по прямой линии в любом направлении. Они не
могут использовать пути, которых нет в их списке.
Поскольку
технология была хорошо усовершенствована, пчелы также изменили свою рабочую
стратегию. Вместо зависания над всеми деревьями в лесу, они нацеливались на
конкретные деревья – преимущественно деревья с большим количеством цветов. Они
планировали, что будут строить новые ульи в таких деревьях. После чего будут
собирать еду только с этих деревьев. Пчелы также удалят некоторые пути со
своего списка, чтобы исключить передвижения к деревьям, в которых отсутствуют
ульи.
Теперь пчелы
хотят построить ульи так, что если вдруг один из путей в их новом списке пропадет
(некоторые птицы или животные побеспокоят их на этом пути), то будет еще
возможно добраться от любого улья к другому, используя существующие пути.
Они не хотят
выбрать менее двух деревьев. Но поскольку строительство улей требует много
работы, они хотят минимизировать их количество. Вам заданы деревья и пути,
используемые пчелами. Вам следует построить новую колонию пчелиных улей для
них.
Вход. Начинается
с количества тестов t (t ≤ 50).
Каждый тест
стартует с пустой строки. Следующая строка содержит два целых числа n (2 ≤ n ≤ 500) и m (0
≤ m ≤ 20000), где n задает количество деревьев, а m задает число путей. Каждая из
следующих m строк содержит два числа u v
(0 ≤ u, v < n, u ≠ v) задающих путь между деревьями u и v. Между деревьями u и v
может существовать не более одного пути, каждый путь во входных данных задается
только один раз.
Выход. Для
каждого теста вывести его номер и количество пчелиных улей, предложенных род
колонию, либо 'impossible' если такую колонию образовать невозможно.
Замечание: Входные данные
большие. Используйте быстрые методы чтения/записи.
|
Пример входа |
Пример выхода |
|
3 3 3 0 1 1 2 2 0 2 1 0 1 5 6 0 1 1 2 1 3 2 3 0 4 3 4 |
Case
1: 3 Case
2: impossible Case
3: 3 |
РЕШЕНИЕ
поиск в
ширину
Анализ
алгоритма
В графе следует найти цикл минимальной величины.
Из каждой вершины запустим поиск в ширину. Пусть например
запущен bfs(i) (0 ≤ i
< n). Встреча в
поиске уже посещенной вершины означает нахождение цикла. Пусть d[j] хранит длину кратчайшего пути от старта i до вершины j. Пусть при проходе по ребру u → v обнаруживается что v уже пройдена (d[v] ≠ INF). Это означает
присутствие цикла длины d[u] + d[v] + 1.
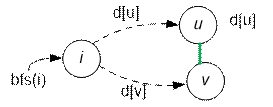
Среди всех найденных циклов находим наименьший по длине.
Пример
Графы, представленные в примере, имеют вид:

Первый и третий графы содержат цикл длины 3.
Реализация
алгоритма
Объявим константу бесконечность INF. Объявим список смежности графа g.
#define INF 2000000000
vector<vector<int> > g;
Функция bfs реализует поиск в ширину из вершины start. В переменной res находим размер минимального цикла.
int bfs(int start)
{
int res = INF;
vector<int> d(n, INF);
vector<int> prev(n,
-1);
queue<int> q;
q.push(start);
Значение d[v] хранит кратчайшее расстояние (по количеству ребер) от вершины
start до v.
d[start] = 0;
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = 0; i < g[u].size(); i++)
{
int to = g[u][i];
if (to == prev[u]) continue;
Если вершина to еще не
посещена (d[to] = INF), то заносим ее в очередь.
if (d[to] == INF)
{
d[to] = d[u] + 1;
prev[to] = u;
q.push(to);
}
Вершина to уже была
посещена. Найден цикл. Имеется путь от start до u длины d[u] и от start до to длины d[to]. На текущий момент встретили ребро
(u, to), образующее цикл. Длина цикла
равна d[to] + d[u] + 1.
else
{
res = min(res, d[to] + d[u] + 1);
Если длина цикла стала равной 3,
то она уже уменьшиться не может.
if (res == 3) return 3;
}
}
}
return res;
}
Основная часть программы. Читаем
входные данные.
scanf("%d", &cases);
for (cs = 1; cs <= cases; cs++)
{
scanf("%d %d", &n,
&m);
g.clear();
g.resize(n);
Читаем ребра графа, строим список
смежности.
for (int i = 0; i < m; i++)
{
int u, v;
scanf("%d %d", &u,
&v);
g[u].push_back(v);
g[v].push_back(u);
}
Запускаем поиск в ширину из каждой
вершины i. В переменной res ищем величину минимального цикла.
int res = INF;
for (i = 0; i < n; i++)
{
res = min(res, bfs(i));
if (res == 3) break;
}
Выводим ответ. Если res = INF, то цикла в графе нет.
printf("Case %d: ", cs);
if (res == INF) puts("impossible");
else printf("%d\n", res);
}
Java реализация
import java.util.*;
public class Main
{
static
ArrayList<Integer>[] g;
static int dist[], prev[];
static int bfs(int start)
{
int res = Integer.MAX_VALUE;
Arrays.fill(dist,-1);
dist[start] = 0;
Arrays.fill(prev,-1);
Queue<Integer> q = new
LinkedList<Integer>();
q.add(start);
while(!q.isEmpty())
{
int v = q.poll();
for(int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (to == prev[v]) continue;
if (dist[to] == -1)
{
q.add(to);
prev[to] = v;
dist[to] = dist[v] + 1;
}
else
{
res = Math.min(res, dist[to] + dist[v] + 1);
if (res == 3) return 3;
}
}
}
return res;
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int cases = con.nextInt();
for (int cs = 1; cs <= cases; cs++)
{
int n = con.nextInt();
int m = con.nextInt();
g = new ArrayList[n];
for(int i = 0; i < n; i++)
g[i] = new
ArrayList<Integer>();
dist = new int[n];
prev = new int[n];
for (int i = 0; i < m; i++)
{
int u = con.nextInt();
int v = con.nextInt();
g[u].add(v);
g[v].add(u);
}
int res = Integer.MAX_VALUE;
for (int i = 0; i < n; i++)
{
res = Math.min(res, bfs(i));
if (res == 3) break;
}
System.out.print("Case
" + cs + ": ");
if (res == Integer.MAX_VALUE) System.out.println("impossible");
else System.out.println(res);
}
con.close();
}
}